Forscher
Triangulation und Theologie

Das gleiche Dreieck als Schlüssel
zur Theologie der Zahlen
in Architektur und Kunst
von Gerhard Becker
Vorwort
Von Schönheit durch Mathematik soll auf den folgenden Seiten die Rede sein, oder anders gesagt von der leider weitgehend vergessenen Kunst durch die Triangulation des gleichseitigen Dreiecks zu harmonischen Verhältnissen, ja edlen Formen zu kommen und zwar in Architektur, Kunsthandwerk und Malerei. Als ich gefragt wurde, wie kommst du dazu an jeden Grundriß und Aufriß das gleichseitige Dreieck anzusetzen, hielt ich im Konvent den Amtsbrüdern ein Kurzreferat als Antwort, ausgehend von der Frage nach Stil und Bauzeit der eigenen Kirche und der anderen dazugehörigen Frage. Wie kommt es eigentlich, daß mittelalterliche Bauten, auch noch die des Barock, ja selbst die Bauten des Klassizismus und schlichte Katen des vorigen Jahrhunderts harmonische Proportionen haben, was man von vielen modernen Bauten nicht sagen kann. Und man kann weiter fragen, wie kommt es, daß etwa neugotische Bauten, selbst wenn alles da ist, Spitzbogen und gotisches Maßwerk, sich diese dem geschulten Auge als nicht mittelalterlich offenbaren. Mit anderen Worten, wo steckt das Geheimnis der Harmonie nach dem unsere Vorfahren bauten? Ist es der goldene Schnitt oder etwas Ähnliches? Sind es bestimmte Zahlenverhältnisse? Wahrscheinlich. Doch solche Zahlenverhältnisse kann nur der aufdecken, der Meter in Fuß umwandelt. Aber welche Fußgröße ist es nun jeweils? Sie schwankte ja zeitlich und regional beträchtlich. Hier galt es, vielen Problemen nachzugehen. Eine Zeitlang war mir die Zeitschrift „Kunst und Kirche“ zugänglich. Mit Interesse las ich darin einen Aufsatz von Heckt über den St. Gallener Klosterplan und einen anderen von Kottmann über die „Hirsauer“. U.a. lernte ich von ihnen, daß man in dieser frühen Zeit christlicher Kirche in Deutschland einen auch in Italien verbreiteten Haussteinfuß von 34 cm und den „pes Liupoldi“, den langobardischen Fuß von 28 cm gebraucht hat, also einen Fuß, der beträchtlich von 30 cm abweicht. Legt man diese Maße bei unseren älteren Kirchen zugrunde, so kommt man in der Tat zu klareren Verhältnisbestimmungen. Außerdem erfuhr ich von dem römischen Baumeister Vitruvius und seinem Werk „De architectura“, das er dem Kaiser gewidmet hatte und das bis in die Renaissance in viele Sprachen übersetzt und immer wieder nachgedruckt worden ist, von der Triangulation als einer Proportionsmethode. Beispiele finden sich in der Vitruvübersetzung von Cesare Cesarino, 1521 (entspr. Gabriel Stornolocho Piacento 1391). Für mich begann nun zunächst in den Mußestunden eine gleichsam aufregende Entdeckungsfahrt zu Vitruv, dessen Werk ich ausleihen konnte. Dann zu Dehio, dem Altmeister der Kunstgeschichte, der sich in mehreren Werken mit diesem Problem befaßt hat, auch zu Architekten des vorigen Jahrhunderts, die ja, wie beim Kölner Dom, mittelalterliche Kirchen zu ende bauten und schließlich zu Architekten und Wissenschaftlern unserer Tage wie z.B. Heckt, Kottmann u. Schubert, von dem noch die Rede sein wird. Übrigens sei hier darauf verwiesen, daß in jüngster Zeit vermehrt Architekten das gleichseitige Dreieck, das Sechseck (Palast der Republik, Berlin) in ihren Entwürfen verwenden. Auch der menschliche Körper wird wie in der Antike versucht zur Grundlage einer Gliederung zu machen (Ronchamp). Bei dem allen wurde mir klarer, daß Kirchenbau verbunden ist mit Theologie. Ich habe darum bei den besonders „beachteten“ beiden mittelalterlichen Theologen Petrus Lombardus und Thomas v. Aquino angeklopft. Besonders der Letztere gab mir dabei Auskunft. Eine Auskunft allerdings so unerwartet fremdartig und doch faszinierend, daß man zwar Mühe hat, sie aufzunehmen, dann aber erkennt, hier ist der Schlüssel für das Gestalten harmonischer Formen und für das Zahlenverständnis der Menschen damals. Hand in Hand ging mit diesen „Entdeckungen“ der Versuch an Grund - und Aufrissen, die mir zur Verfügung standen, zu triangulieren, Proportionen festzustellen, Zahlenverhältnisse aufzudecken. Anhand datierter Gegenstände (Grabsteine, Glocken u.a.) konnte ich eine Aufstellung erarbeiten, die die zeitliche Gültigkeit verschiedener Fußmaße für unseren Raum zeigt. Schließlich, um ein vorläufiges Urteil zu geben, stellte sich immer deutlicher heraus, daß neben anderen Methoden, hauptsächlich die Triangulation nach dem gleichseitigen Dreieck von der Antike bis ins 19. Jahr- hundert hinein als Proportionsgrundlage anzusehen ist. Zweitens, daß für jeden Bau ein ganz bestimmtes Zahlenverhältnis in Koordination zur Triangulation Anwendung fand. Und drittens, daß solche Zahlen voll theologischer Aussagen waren.
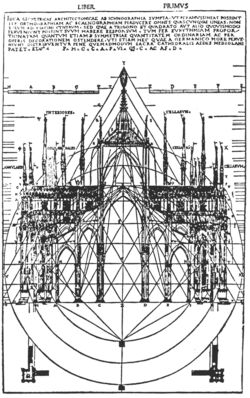
des Mailänder Doms
Georg Dehio, der Altmeister der Kunstgeschichte, soll bei aller Kürze, die ich mir für den Extrakt meiner Arbeit gesetzt habe, zu Wort kommen. In seinem Buch „Ein Proportionsgesetz der antiken Baukunst und sein Nachleben im Mittelalter und in der Renaissance“, Straßburg 1895, weist er auf eine im Handbuch für Architektur Teil IV Bd.1 erschienene Arbeit von August Thiersch hin, der darin (im Blick auf die Triangulation) von der „Entdeckung der geometrischen Analogie der Teile mit dem Ganzen als einer sowohl in der Antike wie in der Renaissance mit klarem Bewußtsein geübten Regel“ spricht. Er berichtet davon, daß besonders praktische Bauleute (Architekten) sich um die Wiederentdeckung der Triangulation bemüht hätten. Er schreibt: „...in der Tat hat es immer einzelne Forscher, insbesondere solche, die von Haus praktische Architekten waren, gegeben, die sich damit nicht beruhigen wollten, daß die Proportionsregeln der Antike mit dem Wenigen, was Vitruv darüber mitteilt, erschöpft waren, und deshalb mit Zirkel und Maßstab selbständig vorgingen“.

Dehio selbst ging nun daran, antike Bauten zu triangulieren, was ihm an Rundbauten gelang, bei basilikalen Bauten aber meist nicht, so daß er zu dem Schluß kam: „...die trianguläre Regel verliert vom Ende des 13. Jhdt. an an Geltung“. Allerdings kannte er sicher die Vitruv-Ausgabe von Rivius, die eine Skizze des Mailänder Domes wiedergab mit einer durchgeführten Triangulation, wo es am 1.5.1392 darum ging, wieweit der Dom höher hinaufgeführt werden könne: „ad quadratum an triangulum“ und man entschied: ipsa posset ascendere usque ad triangulum sive ad figuram triangularem et non ultra“. Dehio weist dann noch auf einen zweiten Beleg für eine durchgeführte Triangulation hin, auf den Kupferstich von 1592, die Kirche St. Petronio in Bologna darstellend. So fragt er schließlich: „...oder hat man die Triangulation gar nicht aufgegeben, sondern diese nur zu einem künstlicheren Verfahren, für das uns einstweilen der Schlüsse noch fehlt, umgebildet?“

Fechtsaal Leyden
Die Suche nach dem „künstlicheren“ Verfahren ist neben und nach Dehio von vielen Architekten, Bauleuten, Wissenschaftlern weiter betrieben worden, wofür eine reiche Literatur spricht. Gewinnbringend war Otto Schubert; Gesetz der Baukunst, Leipzig 1954. Er spricht unter anderem von dem in der Renaissance üblichen Richtungsnetz und von einer zusammen-gesetzten Triangulation, bei der die Dreiecke beliebig oft übereinander geschichtet werden können und handelt bei seinen Versuchen entsprechend. Auch zeigt er als „Schlüsselfiguren“ (die Verschiedenen) meist vom 13. Jhdt. an gebrauchte Grundformen auf. Zufällig entdeckte ich bei Edith Fründ, Reise in den Barock, auf dem Bild des Fechtssaals der Universität Leyden die Schlüssel-figur für die verschiedensten Grundformen.
Nach solchen Erkenntnissen hat Schubert dann auch aus dem Quadrat proportioniert und dabei den Winkel 45 nach p4 zu Hilfe genommen. Ein Triangulationsnetz aber daneben gesetzt, macht dies alles nicht nötig und darüber hinaus eine Zahlenbestimmung nach der Grundzahl möglich, wovon noch die Rede sein wird.
Festzustellen ist, daß nach Vitruv - Rivius s.o. dreierlei legitim erscheint:
- Bestimmung nach Quadrat,
- Bestimmung nach dem gleichseitigen Dreieck
- Bestimmung nach „forma triangularis“, also Formen nach dem gleichseitigen Dreieck.
Zu dem ist nun auch Albrecht Kottmann gekommen, indem er nicht nur den Halbwinkel, sondern auch eine "Scherentriangulation" benutzte, als er mit den lediglich ohne Verbindung angesetzten Dreiecken nicht zum Ziel kam. Kottmanns Arbeiten über frühkirchliche Bauten in Österreich aufnehmend, insbesondere seine Einschätzung zu Hemmaberg, wobei er glaubte feststellen zu müssen, es liege kein geometrisches Vermessungsverfahren vor, führten dazu, einen neuen Ansatz zu erproben.
In der Regel trianguliert man ja von einer Grundlinie aus, wie es Vitruv sagte, aber ein „theologisches“ Herangehen führte dann zum Ziel. Frühe Kirchen wurden in der Regel vom Altar her gebaut. Galt es doch vordringlich den geweihten Altar zu schützen, so stehen noch heute z.B. in Thüringen die Kirchtürme über dem Chor, dem Altarraum. Eine Triangulation vom Altar her war dann durchaus möglich. Wie der Anfang eines Triangulationsnetzes sein kann, zeigt die Skizze, schnell entwickelt sich in der Verlängerung der Schenkel des Grunddreiecks eine Spindel (oder Eieruhr) und mit dem auf das Grunddreieck auf die Spitze gesetzten Dreiecks eine Raute.
- X ist höher als der Kelch, bestimmt aber die Höhe des Fußes.
- Der Halbwinkel (30 Grad) gibt die Basiswinkel ein, 2.Dreieck.
- Das dritte Dreieck auf die Spitze des Grunddreiecks gesetzt, überschneidet sich mit den verlängerten Seiten des 2. Dreiecks. Die Raute gibt die Höhe an.
- Das 4. Dreieck auf die Spitze gesetzt, ergibt die Breite der Kuppa. Mit den Halblinien (30 Grad ) ergeben sich je nach Bedarf des Objekts Basen für weitere Dreiecke.

Bei der Kirche in Eixen / Vorpommern werden auf diese Weise der Sitz des Dreierfensters und die Teilung bzw. Gliederung des Giebeldreiecks festgelegt. Dabei zeigen sich, den Fuß zu 30 cm gerechnet, für Traufe, Kreuz und First in den Maßen der Modulus + (Eigentumszahl) 3x7 verbunden mit der 5: Die Traufe 7, 8 m = 26 Fuß = 3 x 7+5 das Kreuz 15, 3 m = 51 Fuß = 3 x 10 + 3 x 7; der First 18,3 m =61 Fuß = 4 x 10+ 3 x 7.
Folgende Eigentumszahlen befinden sich an den von mir untersuchten Kirchen: 5, 7, 2 x 7, 3 x 7, 8 und 9 (meist bei Klöstern und Priesterpforten). Die 11 fand ich bei Jakobi in Greifwald und dann auch bei anderen Märtyrer-Kirchen. Die 12 bei Leutepforten der alten Kirchen, wie die 10 bei den Herrenpforten und auch die 13, wie zum Beispiel beim Turm der Leester Kirche.

Der Becher aus Kreta ist klar trianguliert. Das gleichseitige Dreieck bestimmt eindeutig die Höhe des Fußes, aber die Kelchschale ist höher als das zweite aufgesetzte Dreieck. Wie kommt man dennoch zu einer Bestimmung? Ausgehend von der Grundlinie setzt man zwischen die begrenzenden aufrechtstehenden Linien als erstes das Grunddreieck, das man durch eine Mittellinie teilt, dann teilt man die Seitenwinkel (30 Grad ) wie es schon an der Zeichnung des Mailänder Doms erkennbar ist und erhält an den Schnittpunkten drei neue Grundlinien. Setzt man nun auf die mittlere ein weiteres Dreieck, so schneiden sich die verlängerten Schenkel mit dem zweiten Dreieck und man erhält die Höhe der Schale. Es entsteht eine kleine Raute, wie man sie an den meisten mittelalterlichen Giebeln auch noch findet, ein Zeichen, dem man unheilabwehrende Kraft zuschrieb.

Erkennbar sind bei einer
Weiterentwicklung außer Christusstern,
Raute und X im Turmbereich
ein weiterer Christusstern.
Nach dieser "verfeinerten Methode" lassen sich Gebäude in Grund - und Aufriß durch das gleichseitige Dreieck in Proportion und Gliederung bestimmen. Die angefügten Beispiele zeigen, daß dies bei schlichten Dorfkirchen wie an Domen und Stadtkirchen geschehen kann. Dabei wird deutlich, das dies auch möglich ist, wo eine Verjüngung (etwa im Aufriß) vorhanden ist, wie es an der Stabkirche von Gol sichtbar ist. Aber auch dort, wo Nebenschiffe oder Anbauten geschehen sind. Hier werden die verschiedenen breiten Anbauten einbezogen. Einmal indem die Verlängerung eines Dreiecks, das die Höhe bestimmt, bis zur Grundlinie durchgeführt wird, zum anderen, daß die Halbwinkel des Grunddreiecks sich über den Rahmen hinaus mit der Verlängerungen der oberen Dreiecke schneiden. So können auch zwei Halblinien dies bewirken, auch neue Basen von Dreiecken, die zur Längen - oder Höhenbestimmung angesetzt wurden. Am Kloster Chorin und auch den Giebeln von Velgast, Neuenkirchen, Groß Kiesow zeigt sich, daß die "verfeinerte Methode" bis ins letzte Detail ortsbestimmend ist. Es erscheint dabei häufig der Christusstern so auch bei vasa sacra und in Gemälden, wenn ein Bezug auf Jesus Christus im Triangulationsnetz gegeben werden soll.

An mehr als hundert Kirchen in Vorpommern und auf Rügen und auch darüber hinaus konnten zunächst einfache Triangulation durchgeführt werden. Festzustellen war dabei, daß bis ins 19. Jahrhundert Grundrisse trianguliert wurden. In der Regel konnte außer dem vollen Dreieck der Halbwinkel angesetzt werden, also wie bei Kottmann, vorgegangen werden. Diese Methode konnte auch bei verlängerter Kathete Anbauten einbeziehen, wie zum Beispiel den Kreuzgang in Jerichow.
Bei den Aufrissen ergab das entwickelte Triangulationsnetz nicht nur klare Bestimmung der Hauptproportionen, sondern an den Fassaden und Giebeln auch die Positionen für Details: Portale, Fenster, Blenden, „Schmuckfriese“, Kreuz und andere Zeichen. Solche Zeichen wurden auch direkt sichtbar im Triangulationsnetz, zum Beispiel A und 0 und X, auch der Christusstern.
Von daher und von der Triangulation Hemmaburgs vom Altar aus wurde die theologische Komponente mittelalterlichen Bauens deutlich. Nicht Architekten allein, sondern auch Theologen waren die Bauleute. Weil dabei die Zahlen und vor allem ihre Bedeutungen wichtig waren, hatten auch die Theologen entscheidend mitzureden. Für sie maßgebend waren die bedeutenden Kirchenlehrer Petrus Lombardus, 1100 bis 1160, und Thomas v. Aquino, 1225/26 bis 1274.
Das bedeutet eine Reise in eine weitgehend unbekannte Welt. Daß die Triangulation mit einer „Festzahl“ für das entsprechende Objekt verbunden sein muß, hat schon Vitruv gefordert. Thomas v. Aquino, der bedeutende Kirchenlehrer und Vater der Scholastik, hat das aufgenommen, wenn er schreibt: „Jeder, der bei seinem Werk ein bestimmtes Maß erstrebt, macht ein Zahlenverhältnis (numerus) ausfindig in den Wesensteilen des Werkes, die an sich zur Vollkommenheit des Werkes erforderlich sind (das gelte nicht etwa für die Zahl der Steine oder Fenster)“.
Weil ja in allen Kulturen Zahlen nicht nur „numerisch“ gebraucht worden sind, sondern ihnen in Zeit - und Kulturbereichen in verschiedener Weise heil - oder unheilbringende Qualitäten zugesprochen wurden, nimmt er auch dazu Stellung. Er geht aus von einer Einteilung der Zahlen in vollkommene Zahl (numerus perfectus), geteilte Zahl (numerus multiplex) und überfließende Zahl (numerus superparticularis). Die 6 ist z.B. eine vollkommene Zahl, denn ihre Teile ergeben wieder eine 6. Die 16 ist eine zusammengesetzte Zahl, weil sie 10 + 6 ist. Die 12 dagegen ist eine überfließende Zahl, weil die Teile nicht 12, sondern 16 ergeben. Die Teiler der 12 sind 1, 2, 3, 4 und 6; die Summe ergibt 16. l und 3 sind vollkommene Zahlen. Sie gehören zu Gott, der aller Dinge Maß, Zahl, Ordnung und Ziel ist: omnia creata ordinantur in Deum.
Thomas von Aquino sagte dazu: „Die Artgestalt der Dinge sind die Zahlen, die durch Hinzugabe oder Wegnahme einer Einheit in der Artgestalt abgewandelt werden.“
Das Triangulationsnetz, das ich auf dem Weg zu „künstlicheren Formen“ so entwickelte, daß vom Grunddreieck aus durchgehend das Dreieck und sein Halbwert angesetzt wird, zeigt an den Schnittpunkten nicht nur am jeweiligen Objekt markante Punkte für Gliederung und „Dekor“ und z.B. den Ort für Fenster am Bau oder für die Gliederung des Giebels an, sondern läßt Zahlen zur Aussage kommen, sobald man das Fußmaß eingegeben hat. Beispielhaft ist dies an der Pforte vom Kloster Chorin erkennbar: Die 9 und die 5 (Gebet zum Dreieinigen Gott und Maria, Patronin der Benediktiner und Zisterzienser) weisen den Bau als Teil eines Zisterzienserkloster aus. Im Aufriß läßt sich die 3 x 5 auf Gott und Maria die Gottesmutter erkennen, die 9 Blenden darüber und die 3 Rosen in den Giebeln. Doch das ist nichts Einmaliges. Hier wird besonders eindrücklich, wie die Theologie das Bauwerk prägte.

Ähnlich ist auch das Beispiel der Annen - Kapelle in Greifswald. Und um zu zeigen, daß diese von der scholastisch beeinflußten Theologie bestimmte Art des Bauens auch im sogenannten weltlichen Raum geübt wurde, steht das Steintor in Anklam.
Die 10 als Zahl göttlicher und irdischer Macht bzw. Kraft bestimmt das 33 Meter hohe Tor in seiner Gliederung, wobei die Wehrgangzone noch besonders herausgenommen wurde und schließlich auch den Giebel, dem die Zahl 8 als das Feindliche, Böse abwehrend eingegeben wurde und zwar in den drei Stufen verbunden ist mit der 4, der 12 und der 21. Zu deuten auf die Evangelisten, die Apostel und alle Heiligen, deren Fürbitte man mit dem steingewordenen Gebet (Giebel) erbitten wollte.

Leeste, Querschnitt
Thomas von Aquino nennt:
numerus sesqui altera 1 + 1/2
numerus sesqui tertia 1 + 1/3
numerus duplex sesquialter 2 + 1/2
numerus triplex sesquialter 3 + 1/2
numerus quadroplex sesquialter 4 + 1/2
numerus duplex sesquitertia 2 + 1/3
numerus duplex sesquiquarta 2 + 1/4
numerus duplex suparbipartiens 2 aber eine 2 bleibt
numerus duplex tripartiens 3 aber eine 3 bleibt
Das sind Zahlenverhältnisse wie sie bei uns kaum gebräuchlich sind und bei denen wir „Harmonie“ nicht vermuten würden. Dennoch fanden sie Anwendung und können unsere nur vagen Verhältnisbestimmungen, etwa 1 zu 2 oder ähnliches korrigieren. Sie finden sich sie beim Triangulieren des Kirchturms in Leeste.
Die heutige Kirche ist erst 1777 erbaut worden, der Turm allerdings im unteren Backsteinmauerwerk ist älter und im Turm überrascht der Hausbaum auf dem flachen Granit. Die Geschosse, nach Meter gemessen, zeigen ungleiche Höhen. Umgerechnet aber auf das Fußmaß hin, das aus Daten des Vorgängerbaus und des Turms ermittelt wurde, kommt es zu den komplizierten Daten scholastischer Art.
Nun noch zu den Zahlen, die mehr als nur mathematische Größen waren. Zunächst sei noch einmal darauf hingewiesen, daß bei der Proportionsbestimmung jeweils eine bestimmte Zahl für das Objekt festzulegen ist. So ist auch in der Literatur von solchen Zahlen die Rede, etwa daß für den Kölner Dom die 25 bzw., die 50 bestimmend sei. Kaum aber ist die theologische Wertigkeit dieser Zahlen beachtet worden. Erst bei Thomas v. Aquino, dem Meister der Scholastik, ist zu erfahren gewesen, wie aussagekräftig die Zahlen sind.
Die drei Beispiele seien Beleg dafür.
An der Pforte des Kloster Chorin dominiert die 9 bzw. 3 x 3 als Zahl des Gebets zum dreieinigen Gott, des Priestertums (die Priesterpforten unserer alten Kirchen haben diese Zahl) und des Klosters. Ebenfalls ist die 9 an der Klosterpforte zu finden. Dazu kommt die 5 als die Marienzahl (fünfblättrige Rose). Da wo das Rosensymbol im Mauerwerk erscheint, ist die Höhe auch bestimmt von der 5. Maria war die Patronin der Benediktiner und Zisterzienser. Ihr gehörte das Kloster. Wenn in der Breite und in der Höhe die 8 dazu kommt, so deshalb, weil dieser Zahl Macht dem Bösen gegenüber zugeschrieben wurde, aber positiv auch Reinigung und Reinheit bewirkte. Der Jungfrau Maria waren daher oft 5 und 8 zugeordnet.
Bei der Annen - Kapelle ist die 12 dominant, die als Zahl der Apostel und der Gemeinde oft erscheint. Wie läßt sich das auf den Weihetitel hin erklären? Wenn das Portal für die Priester, die Priesterpforte, wie eben gesagt, die 9 hatte, so hatte das Hauptportal, die Herrenpforte, die 10 als Zahl der Macht und das Portal für die Gemeinde, die Leutepforte, die 12. Die Annen - Kapelle aber steht vor der Leutepforte und die zweite Zahl, die 4, die Kreuzblume, weist auf den Weihetag der Kirche hin, der für die frühen Kirchen im Missionsgebiet Kreuzerhebung war. An Christi Tod am Kreuz und seine Auferstehung will das, was wir als „Dekor“, als Schmuck betrachten, erinnern.
Zu erwarten ist beim Steintor, dem dritten Beispiel, die 10. Das Zeichen für irdische und göttliche Stärke und Macht. In der Multiplikation wird die Fassade bis zur Spitze gegliedert. Bis über der8 x 10 der Giebel zu einem großen orate pro nobis, ein Gebet um Fürbitte wird. Zur 80 hinzugefügt wird die 4. Zu deuten auf die Evangelisten, die 12 bei der 2. Stufe. Hier werden die Apostel angerufen. In der 3. Stufe dürften mit der 21, den 3 x 7, alle Heiligen gemeint sein. Gottes Macht und Schutz wird erbeten und in der 3 soll Gott nach ihrem Verständnis gegenwärtig sein und im Kleeblatt, mit dem die Blenden abschließen, und den Kreuzblumen soll Christi Opfer helfen gegen alle bösen Mächte, die man sehr real gegenwärtig wußte. Die 8 sollte verbunden mit Gottes Macht (10) alle Gefahren abwenden. Und das alles sollte zur rechten Harmonie des Bauwerks führen.
Sagte doch Thomas v. Aquin: Das letzte Endziel eines jeden beliebigen Geschöpfes aber ist, daß es die göttliche Ähnlichkeit erlange. Und mit Augustin sagte er: Die Dinge werden durch Zeichen erkannt, also ist jedes Zeichen auch irgendwie das Ding. (res etiam per signa discuntur. Omnis igitur signum etiam res aliqua est.)

Thomas v. Aquino:
1. „Jeder, der bei einem Werk ein bestimmtes Maß erstrebt, macht ein Zahlenverhältnis (numerus) ausfindig.“ (so lehrte es auch Vitruvius)
2. „Die Artgestalt der Dinge sind die Zahlen, die durch Hinzugabe oder Wegnahme in der Artgestalt abgewandelt werden.“
3. Er wendet sich gegen Bilderverehrung, räumt dann aber ein: „... weil aber die Figuren in den künstlichen Dingen gewissermaßen artbildene Formen sind, kann jemand sagen, nichts hindere, daß auf die Erstellung einer Figur...irgendeine Wirkkraft aus himmlischen Einfluß folgt“.
Zu 1. Will man Eurythmie erreichen, muß unbedingt die Schlüsselzahl (numerus) bei der Proportionierung eines Gegenstandes zum Zuge kommen. Die Schlüsselzahl findet man in der Regel aber bei allem, was vor der Einführung des Dezimalsystems entstanden ist, erst nach Feststellen des jeweiligen Fußmaßes. Bei Backsteinbauten ist festzustellen, daß 3 Schichten + Fuge dem Fußmaß des Baues entspricht. Das man kompliziertere Verhältnisse kannte, als wir sie kennen, zeigt der Leester Turm. (siehe Zahlenverhältnisse bei Thomas v. Aquino)
Zu 2. Nach diesem Grundsatz, nämlich durch Zusatz abgewandelter Zahlen kommt nun z.B. bei der Pforte, Chorin und dem Steintor, Anklam zur Schlüsselzahl (numerus) die 8 als unheilabwehrend bzw. reinigend hinzu, so auch bei Fünten. Die Kreuzzone am Giebeldreieck an der Kirche in Eixen hat nicht wie ich erwartete die 4 x 7 wie üblich, sondern die 3 x 10 als Zeichen des allmächtigen dreieinigen Gottes.
Zu 3. Diese Stellungnahme dürfte zur Tolerierung des aus dem Heidentum überkommenen Wertung „heiliger Zahlen“ geführt haben. Alte heidnische Zeichen an christlichen Kirchen (Siehe Eixen) hat man sicher umgedeutet, etwa 2 mal das gleichseitige Dreieck, also heiliger Bezug zum dreieinigen Gott. Daß man von ihm eine besondere Wirkung erwartete, sah man als erlaubt an. Die Zahlen sind die Dinge, so hat es Thomas v. Aquino von Platon übernommen, und so traute man den Zahlen Macht zu, zum Bösen, von dem man sich allezeit bedroht fühlte, aber auch von anderen zum Guten, zu Hilfe und Schutz. Auch diese Tatsache muß man sehen, wenn man „überkommenen Kulturgut“ gerecht werden will. Die Reformation allerdings bekämpfte diese Anschauung, was sich dann auch in der Wertung dieser Zahlen als Aberglaube mehr und mehr durchsetzte.
Für unsere Vorfahren waren Zahlen also nicht nur Mittel, harmonisch zu gestalten, sondern sie gaben auch Auskunft über Zweck und Eigentümer (ob der Gegenstand zu einem Kloster, oder einer Kirche gehörte) und über die Funktion (Glocke oder Fünte). Damit wird Dehios Vermutung bestätigt, daß ein künstlicheres Verfahren, das gleichseitige Dreieck zur Proportionsbestimmung anzuwenden, zum Ziel führt. Allerdings sei noch einmal festgestellt, daß nach Rivius - Vitruv drei Verfahren in Übung waren: Das gleichseitige Dreieck, die forma triangularis und das Quadrat, auch daß Schubert darauf hingewiesen hat, daß viele Grundformen außer dem gleichseitigen Dreieck angewendet wurden. Die Schlüsselfigur im Fechtsaal war ja eine Hilfe dazu für den Praktiker. Das Triangulationsnetz aber ist allein von Winkeln her (60, 45, 30, 15, 7, 5 Grad) schon in anderen Grundformen präsent und gibt als Netz Angaben über Einzelheiten und läßt die eingegebenen Zahlen erkennen und zur Aussage kommen. Dies wurde an Bauten kurz in Wort und Beispiel deutlich.

Ein staatlicher Befehl führt zu weiteren Entdeckungen. Die Kirche sollte ihren Kulturbesitz erfassen und melden. Bei der Durchführung dieses Auftrags wurde auch ich tätig und hatte so in vielen Gemeinden Glocken und Taufsteine und alle vasa sacra (Kelche, Leuchter, Kannen u. anderes) zu bestimmen, wenn möglich zu fotografieren und zu vermessen. Selbstverständlich versuchte ich auch die Triangulation anzuwenden, einfach zur Stütze für das, was ich inzwischen "entdeckt" hatte. Und in der Tat, auch Fünten ließen sich triangulieren und gaben nach Umrechnung in Zoll kund, zu welcher Kirche sie gehörten, deren Eigentumszahl, bei Jakobi die 11, bei Marien in Anklam die 5. Sie waren also nicht nur bestimmend in Grund- und Aufriß, sondern auch beim "Inventar" und durch die Zugabe von Zahlen wurden jeweils auch Funktion bzw. Gebetsanliegen ausgedrückt, zum Beispiel in Anklam durch die 8 der Abwehr des Bösen und die Gabe der Reinigung. Auch von den Glocken ließ sich dieses feststellen. Ein besonders schönes Beispiel bietet die große Kriener Glocke.
Es haben also nicht nur die Gebäude ihre vollendete Harmonie durch das gleichseitige Dreieck verbunden mit "heiligen" Zahlen bekommen. Das es auch für Kelche, Leuchter u.a. gilt, erwies sich, als ich die Daten der Objekte von der Skizze ins Reine bringen wollte und diese Zahlen in das Triangulationsnetz eingab. Wie dabei verfahren wurde, läßt sich am ältesten Kelch aus der Krypta in Speyer zeigen.
Die Methode dort hat weiter Anwendung gefunden und war schließlich in der Gotik zu einer "Norm" geworden, nach der die Meisteranwärter ihr Meisterstück nach dem in der Lade aufbewahrten Stück zu machen hatten. Künstler schufen besonders in der Renaissance Vorlagen, nach denen der Goldschmied arbeitete. Von Schinkel ist ein Entwurf bekannt, nach dem der bekannte Goldschmied Hossauer einen Kelch verfertigte.
Wer kannte die Kunst?
Zu den vasa sacra zähle ich im weitesten Sinn auch Taufsteine und Glocken, Leuchter und Weinkannen neben den eigentlichen vasa sacra, den heiligen Geräten. Zu den Taufen muß angemerkt werden, daß nur wenige der alten Fünten noch am alten Ort, dem Kinderhaus oder Taufhaus sich befinden. Die mittelalterlichen Taufsteine aus gotländischem Kalkstein, auch dort entstanden, mußten weitgehend im 18. Jahrhundert moderneren weichen. Weil sie nicht aus einem Stück entstanden waren, sondern Fuß, Schaft und Kuppa für sich gefertigt wurden, konnten sie erst in unserer Zeit, oft nur die Kuppa, und leider oft falsch zusammengesetzt in die Kirchen zurückkehren. So ist es auch in Anklam in der Marienkirche geschehen, wo heute noch dem großen Taufstein das Mittelstück fehlt, das ich allerdings zeichnerisch ergänzt habe, um eine Triangulation zu wagen. Vollständig dürfte der Levenhagener Taufstein sein, bei dem die eingebundenen Zahlen auch in Zeichen erscheinen.

Die 4 findet sich im Fuß und die 12 in der Kuppa mit den Aposteln. 4 als Sinnbild der Evangelisten bzw. der 4 Lebensströme und die 12 als Zahl der Apostel, der Gemeinde Christi. Vollständig, weil aus einem Stück sind die alten Granitfinten. Die Taufe aus der Jakobikirche in Greifswald hat die 11 als Hauptzahl, welche auch die der Kirche ist und vorausgreifend auch am gotischen Kelch sich findet. Daß sich die Zugehörigkeit zu ihrer Kirche in Zahlengleichheit mit dieser zeigt, was selbst für die Grabsteine z.B. so in Nikolai in Greifswald gilt, ist überraschend und ein Beleg dafür, daß man die vasa sacra nicht "nach Katalog" anschaffte.
Kurz etwas zu den Glocken. Die Beispiele, die ich vermessen und triangulieren konnte, geben zu erkennen, daß das Prinzip aus einer Raute heraus die Gliederung zu bestimmen, bis in unsere Zeit beibehalten wurde. Das dürfte nicht nur eine Frage der Tradition sein, sondern auch daher kommen, daß die Glocke als Klangkörper ein Höchstmaß an Vollendung zeigt. Als Zahl erscheint die 12, wobei für mich noch offen bleibt, ob dies die Zahl der Kirche, zu der sie gehört oder die ihres Amtes, zur Gemeinde zu rufen, ist.
Zu den Kelchen. Soweit sie Goldschmiedearbeiten sind, stehen sie in Tradition vom Altertum her. Sie sind gegliedert in Fuß, nodus und cuppa. Zunächst in romanischer Zeit gedrungen wie der Kelch aus der Krypta von Speyer, dann gestreckt in gotischer Zeit bleiben sie das Vorbild für den Abendmahlskelch, wenn ein Geselle ihn als Meisterstück zu machen hatte. Und wenn Künstler Kelche für den zivilen Gebrauch entwarfen, siehe Altdorfer und Schinkel, so ließen sie ihre Phantasie wohl walten, doch ohne die Grundform und Gliederung aufzugeben in Fuß, nodus und cuppa. Übrigens die Tatsache, daß die Goldschmiede nach Entwürfen von anderen arbeiteten, könnte vorsichtig dahin gedeutet werden, daß den Goldschmieden und anderen Kunsthandwerkern die Gesetze einer "künstlerischen Triangulation" nicht allgemein bekannt waren.

aus Troja
War bei den Grundrissen ein einfaches Triangulationsnetz ausreichend zur Bestimmung der Proportionen, mußte bei den Aufrissen, den Fassaden und Giebeln das Netz enger werden, um alle Details zu erfassen.
Bei den vasa sacra hat ein weiterer Schritt getan werden müssen. Es galt die Gliederung des Fußes bei Fünten, Kelchen und Leuchtern zu bestimmen. Das ist zwar durch Teilungen an der Basis des Grunddreiecks möglich, ich habe aber nach unten hin, über die Hypothenuse trianguliert. Die ausladenden Tüllen und Henkel bei den Kannen lassen sich durch Halbwinkel - Katheten zum Schnittpunkt bis zu anderen Katheten bzw. Waagerechten (Hypothenusen) führen und sind so bestimmend.
Bei den Kelchen zeigt sich, daß die Goldschmiede traditionell noch lange den "gotischen Kelch" von den Meisteranwärtern forderten, während die Zinngießer in reicher Vielfalt ihre Werke schufen. Bei den Kannen fällt auf, daß sich der Keramikkanne aus Troja gleichsam als Vorläufer der noch heute beliebten Kannen darstellt, nur daß sich materialbedingt kleine Änderungen zeigen und auch der Körper auf einen Fuß gesetzt wird.
Ein weiteres Kapitel ist das einer Triangulation an Ge-mälden. Daß die von Vitruv als gebräuchlich angesehene Methode auch auf diesem Gebiet menschlichen Schaffens schon in früher Antike angewendet wurde, sehe ich im "Familienbild des Echnaton" geschehen. Die Art wie hier das Triangulationsnetz den Bezug der Assistenzfiguren zur göttlichen Quelle festlegt, wurde weiter geübt wie z.B. etwa bei Ikonen, ja noch von Raffael in seiner bekannten Mariendarstellung, und das neben exakter Festlegung auch im Detail. In der Renaissance fand die Methode Anwendung in der Architektur wie schon erwähnt, aber auch die Maler z.B. Dürer, Altdorfer, Cranach und andere nutzten das Triangulationsnetz.
In der Buchmalerei und an Altären findet man es. Bei Meister Bertrams "Krippenbild" entspricht die etwas gezwungene Haltung der Maria dem Triangulationsnetz Wie lange bedienten sich noch nach der Renaissance Maler dieser Methode? Rembrandt tat es sicher, wie die Beispiele zeigen möchten. Reste einer Triangulation auf die er dann sein Bild malte bzw. mit dem Stichel zeichnete, lassen sich erkennen, wie ich meine. Auch Tischbeins Goethe ist in ein Triangulationsnetz gemalt. Bei Runge erwartete ich es nicht mehr, der Sechsstern aber machte mich stutzig. Ganz deutlich ist von ihm aus die ganze Gruppe trianguliert. Überrascht war ich schließlich, als sich selbst bei Monet bis in Details eine Triangulation durchführen ließ, wie ebenfalls bei Richter. Schließlich dürften die weiteren Bilder zeitgenössischer Maler (Modigliani, Picasso, Matisse) zeigen, daß ihnen die Methode nicht unbekannt war.
Eine Untersuchung der Maßverhältnisse mittelalterlicher Grabplatten (nach v. Haselberg) ergibt für den Raum Greifswald folgendes Bild: Die ältesten Platten in Marien, Greifswald lassen sich nach dem Fußmaß 33,5 cm; 32,2 cm; 33,7 cm messen. Dies ist der alte „Haussteinfuß“ vieler unserer Feldsteinkirchen des 13. Jahrhunderts. Die älteste Platte in Jakobi von 1323 hat den Fuß von 29 cm. Mehr als 20 Platten im Raum Greifswald haben bis über die Mitte des 14. Jahrhunderts dieses Maß. Von der Mitte des 14. Jahrhunderts an (Marien, Greifswald), verstärkt ab letzten Viertel, mißt der Fuß 30 cm. Auch hier lassen sich etwa 20 Platten so messen. Von der Mitte des 15. Jahrhunderts an vergrößert sich das Maß auf 30, 5 cm (1450 Nikolai, Greifswald), vielleicht schon 1413 in Eldena nachzuweisen. Im 16. Jahrhundert beginnt der „Pommersche Fuß“ sich durchzusetzen (Marien, Greifswald 1517, Maß 28, 8 cm - 29, 5 cm). Außerdem findet sich in diesem Zeitraum bei den untersuchten Platten einige Male der Fuß zu 28 cm, so 1417 Marien und Jakobi, Greifswald, und schon früher Marien, Greifswald 1388. Auch der Fuß von 31,2 cm findet sich in Jakobi, Greifswald, Fünte, und 1388 in Marien. Grabsteine wurden wiederverwendet. Das kann die Datierung erschweren. Diesem Ergebnis entspricht die Datierung die Frau Mehnert den mittelalterlichen Taufsteinen im vorpommerschen Raum gab, mißt man den oberen Durchmesser. Die Taufsteine des 13. Jahrhunderts haben 33,5 cm als Fußmaß (Altenkirchen und Vorland). 34-35 cm Fußmaß findet sich in Sassen, Görmin, Grimmen, Altefähr, Brandshagen, Dersekow, Wehrland, Gustow und Waase. 31,2 cm Fußmaß mißt Behrenhof, Loitz, Rambin, Kenz, Jakobi, Greifswald und Voigteshagen. 32,2 cm Fußmaß mißt Wusterhusen, Rappin und Horst. Um 1300 haben wir noch in Kartlow 33,7 cm, aber auch Sanzkow mit 30 cm. Der Fuß zu 30 cm als altes Maß kommt neben anderen schon früh auf, besonders beim Backstein. Anfang 14. Jahrhundert tritt aber auch bei Fünten das Maß 29 cm auf (29,5cm, 28,7cm). So in Marien, Anklam, Stoltenhagen, Stargard/Mkl., Jakobi in Stralsund. Dazu dürfte auch Levenhagen gehören (29,2 cm), die Frau Mehnert Mitte 14. Jahrhundert datiert, doch hier ist auch 32,7 cm möglich. Auf 1331 datiert sie auch im Blick auf eine Urkunde die Taufe von Kröslin, die den Fuß zu 30 cm hat. Ins 14. Jahrhundert verweist sie denn Bergen/Rügen mit dem gleichen Fuß, auch Reinberg kann dazu gehören. Schließlich wären noch die Glocken zur Datierung heranzuziehen. Das Material ist recht spärlich. Die meist undatierten alten Glocken haben Maße wie 34 cm, 32 cm, 31,5cm; 31cm, 25 cm. Die des 16. Jahrhunderts haben 27,5 cm, 28cm, 29;cm, auch 30 cm, was sich weitgehend als Backsteinmaß ausgibt.
Zusammenfassend läßt sich sagen:
Das Fußmaß des 13. Jahrhunderts variiert, neben 30 cm gibt es das Haus/Feldsteinmaß von 31,2 cm bzw. 32 - 35 cm. Im 14. Jahrhundert wird es abgelöst durch das kleinere Maß 29 cm, das gegen Ende auf 30 cm anwächst.
Zu Beginn des 16. Jahrhunderts wird dieses Maß, das gegen Ende des 15. Jahrhunderts noch auf 30,5 cm kommt, wieder durch ein kleineres von 29 cm abgelöst, was dem Pommerschen Fuß entspricht, für den ich zwei Angaben fand: 1. Bei Baumstark, Die Universität Greifswald vor 100 Jahren 1866: 1 F = 12,9 Pariser Linien = 0,902 rhein. F = 0,28309 m, und 2. Ausgabe im Amtsbl. Kgl. Reg. v. 1899 = 0,292058 m. Im 19.Jahrhundert galt der Preußische Fuß mit 31,39 cm.
Eine Kurzfassung ist das, was ich jetzt niedergeschrieben habe. Ich weiß, eine Kurzfassung hat bei viel Positivem auch leicht die Nebenwirkung, daß sie dem Leser mehr zumutet als zumutbar ist und sein soll; zumal bei einem Objekt, das doch zunächst sehr fremd erscheint. Begonnen hat mein Interesse und Forschen, wie ich schon anfangs sagte, mit der Frage nach der Baugeschichte „meiner“ Kirche. Auf der Suche nach einschlägiger Literatur konnte ich Arbeiten kennenlernen und Anregungen gewinnen. So versuchte ich auch das gleichseitige Dreieck an Grund- und Aufrissen anzusetzen. Dabei benutzte ich auch den Teilwinkel von 30 Grad. Triangulierte wie schon die Baumeister der Renaissance am Mailänder Dom kombiniert mit Quadrat und Winkeln, um zum Ziel zu kommen. Schließlich beschränkte ich mich aber bald auf das gleichseitige Dreieck, das sich gleichsam „organisch“, nicht durch beliebiges Setzen eines anderen Dreiecks, zum Triangulationsnetz erweiterte, das nun nicht nur die großen Proportionen bestimmt, sondern bis ins einzelne Detail ortsbestimmend ist, wenn man das nach Vitruv, zunächst festgelegte Grundmaß (Zahl) weiter beachtet. Wo das nicht geschieht, etwa bei einer Restauration oder Erweiterung geht das auf Kosten der „Eurythmie“ und „Symmetrie“, die schon Vitruv bzw. die antiken Baumeister anstrebten, so daß ihre Werke heute noch von unübertroffener Schönheit sind und in der Landschaft nicht als Fremdkörper wirken. Wie weit wurde nun über die Renaissance hinaus diese Methode angewendet? Es geschah noch im 19. Jahrhundert, als Beispiel weise ich auf die Kirche in Alt Pansow hin, aber auch Kapellen im Kreis Anklam sind mir bekannt geworden.
Ich hoffe, mit dieser Kurzfassung über den Schlüssel zur Harmonie durch Dreiecke und Zahlen, ein wenig neugierig gemacht zu haben.
Wer nun Lust bekommen hat, auch einmal hinter das Äußere schöner Dinge zu schauen, der versuche es doch mit der „forma triangularis“, wie ich sie über Jahrzehnte erprobt und nun beschrieben habe.
Recht einfach läßt es sich an Grundrissen tun, wie die Beispiele es zeigen. Komplizierter wird es bei Aufrissen doch auch interessanter, weil wir z.B. die Gliederung von Giebeln entdecken, und darüber hinaus erfahren, wie ganz bewußt Zahlen eingegeben wurden, die etwas aussagen wollten. Welche Mühe und welchen Fleiß haben die Bauleute und Theologen es sich kosten lassen, ihr Werk in Einklang zur Schöpfung zu schaffen, weil ja auf Gott hin alles Geschaffene zielt. (Siehe Thomas v. Aquin) Doch auch an schönen Dingen um uns in der Wohnung lohnt sich ein Versuch. Vielleicht überrascht werden wir feststellen, daß der schöne Pokal oder Leuchter oder die Kanne ja durch das darüber gelegte Triangulationsnetz sein Geheimnis der Harmonie preisgibt. Auch bei vielen anderen Werken des Kunsthandwerks und der Malerei werden wir entdecken, daß ganz sichtbar, z.B. bei Runge und Matisse das gleichseitige Dreieck bzw. der Sechsstern die Komposition beeinflußt.
Uns allen aber, die wir uns noch immer freuen an einem alten Bauernhaus oder einem Weinkelch, aus dem wir bei festlichem Anlaß trinken oder dem Milchkännchen im „Hofstil“ beim Frühstückskaffee, erfahren nun, warum uns dies so besonders anrührt und gefällt. In unserer Zeit mit ihrer explosiven Entwicklung in Wissenschaft und Technik droht ja unser Menschsein in Anbetung falscher Idole unermeßlichen Schaden zu nehmen, so daß viele Zuflucht suchen bei anderen Kulturen. Da ist es gut zu erfahren, daß unsere Quellen da sind, wo unsere Vorfahren mit großem Ernst und Fleiß im Einklang mit der Schöpfung und dem Schöpfer ihr Tun und Wirken zu erfüllen suchten. Denn so sagte es Thomas v. Aquino: „omnia creata ordinantur in Deum.“ (Alles ist auf Gott hin geordnet.) Und der Kirchenvater Augustin bekannte: „cor nostrum imquietum est donec requiestcat in te“. („Unser Herz ist unruhig bis es Ruhe findet in dir.“)
Arens, F. V.: Das Werkmaß in der Baukunst des Mittelalters 8.-11. Jhdt., Diss. Bonn, Würzburg 1938
Baltzer; Wagrien: Ein Beitrag zur Entstehungsgeschichte der Ziegelbaukunst in Lübeck; in Zeitschrift des Vereins für Lübeckische Geschichte und Altertumskunde Bd. 23, 1926
Bandmann, Günter: Die Bauformen des Mittelalters 1949
Booz, P.: Der Baumeister der Gotik, München Berlin 1956
Bosiker, M.: Von der Fialengerechtigkeit 1486
Reichensperger, A.: Der Christliche Altar 2.Bd. 1924
Braun, J.: Ein Proportionsgesetz der antiken Baukunst und sein Nachleben im Mittelalter und in der Renaissance, Straßburg 1895
Dehio, Georg: Die Kirchen des Zisterzienserordens in Deutschland während des Mittelalters,
Diss. Göttingen 1868
Dohme, R.: Die Marienkirche zu Greifswald 1956 Chr. Denkmal 2.Aufl. 1962
Fait, Joachim: Reise in den Barock, Prisma VLG. 1972
Fründt, Edith: Die frühe Kirchenbaukunst der Zisterzienser, Berlin 1957
Hahn, H.: Der Kirchenbau des Mittelalters in Handbuch der Architektur
Hasak, Max: Das St. Galler Klosterplan-Schema in Abhandlung der Braunschweigischen Wissenschaftlichen Ges. Bd. 17, 1965
Hecht, Konrad: Kirchen auf dem Lande, EVA Berlin
Holz, Gottfried: Chorin - Gestalt und Geschichte eines Zisterzienser Klosters, Leipzig 1962
Kesting / Schneider / Groß: Zisterzienser Kloster Eldena, Berlin 1929
Kloer: Geschichte des deutschen Kunsthandwerkes 1955
Kollhausen, Heinrich: Maßverhältnisse in Bauten der Hirsauer, Hirsau im Schwarzwald, 3.Aufl. 1967
Kottmann, Albrecht/ Schloß, Helmut: Der frühe deutsche Kirchenbau 1938
Lehmann, Edgar: Deutsche Goldschmiedekunst 1954
Leitermann, Hans: Die mittelalterlichen Taufsteine in Vorpommern, Diss, Greifswald, 1934
Mehnert, Annemarie: Das mittelalterliche Kirchenportal in Vorpommern, Diss. Stettin 1937
Möller, Herbert: Die Marienkirche zu Bergen auf Rügen, in Das christl. Denkmal 1962
Ohle, Walter: Das Kloster Chorin in der Reihe: Das christliche Denkmal 1965
Prange, Georg: Geschichte des Zisterzienserklosters Eldena, Greifswald 1882
Pyl, Theodor: Der Kirchenbau in Mecklenburg und Neuvorpommern zur Zeit der deutschen Kolonisation, Diss. Pom. Jahrb. Erg. Bd. 2 Greifswald 1910
Reifferscheid, Heinrich: Sinnzeichen des Glaubens, EVA 1954
Rietschel, Christian: Symbolik des Kirchengebäudes 1924
Sauer, Josef: Die Kirchenbauten Mecklenburgs, Schwerin 1927
Schmalz, Karl: Kunstdenkmäler des Kreises Grimmen, Grimmen 1931
Schmitt, Otto: München und Zürich, Langobardische Baumeister in Lorsch und Hirsau, 1965
Schnell, Steiner: Gesetz der Baukunst, Leipzig 1954
Schubert, Otto: Das Proportionswesen der Geschichte der gotischen Baukunst und die Frage der Triangulation
Thomae, Walter: Nach rechtem Maß, Untersuchungen zum Proportionsbegriff des 13. - 16. Jhdt.
Ueberwasser, W.: Jahrbuch preuß. Kunstsammlungen 1935
Haselberg, Lemke von: Die Denkmalpflege 29.Bericht 1929
Velte, Maria: Die Anwendung der Quadratur und Triangulatur bei der Grund - und Aufrißgestaltung got. Kirchen, Basel 1951
Vitrivius: De Architectura Lipsiae, 1912
Vitruvius: Pollio, de architectura durch Rivius 1614
Wimmer, O.: Handbuch der Namen und Heiligen 1959 / Heidelberg 1933
































